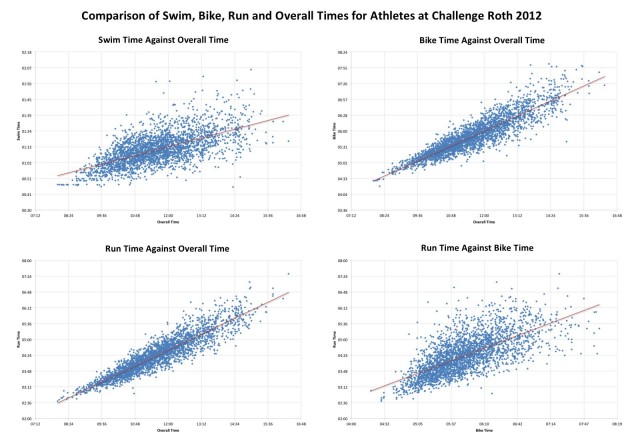
I’ve not quite finished. A couple of months back I examined the results from Challenge Roth – retrieved far more easily, complete with splits – to look at the relationship between bike and run performance across the field. I was interested to see if that data backed up the notion that age groupers who bike too hard pay a price on the run. My initial conclusion at the time was shockingly that faster athletes are faster. Scatter graphs from Roth results (below) show the distribution between splits in swim, bike and run with overall times and gave a hint towards the degree of correlation.
Each comparison has a trend line in red giving an indication of the kind of relationship; in each case faster finish times come from faster splits. Faster athletes go faster. The degree of scatter around the best fit line gives some indication as to the strength of the correlation; for example, in Roth, any correlation between swim performance and finish time is weaker than any correlation between run performance and finish time. Not that correlation is necessarily cause. Unsurprisingly repeating the process for Kona shows similar results.
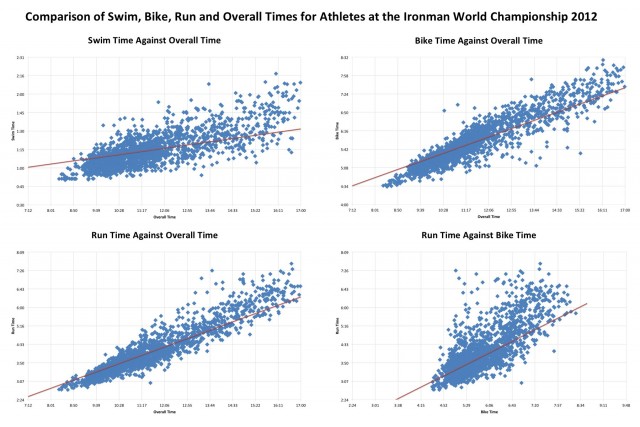
Faster athletes are faster at the World Championship too. The relationship seems a little tighter too – less dispersal when comparing swim times and finish times, or run times against bike times. Perhaps the result of the selective entry criteria for the majority of athletes: qualification removes the weakest swimmers, cyclists and runners. Having to qualify means that you cannot afford to have a genuinely weak discipline, there is variance, but in relative terms these athletes are quite balanced.
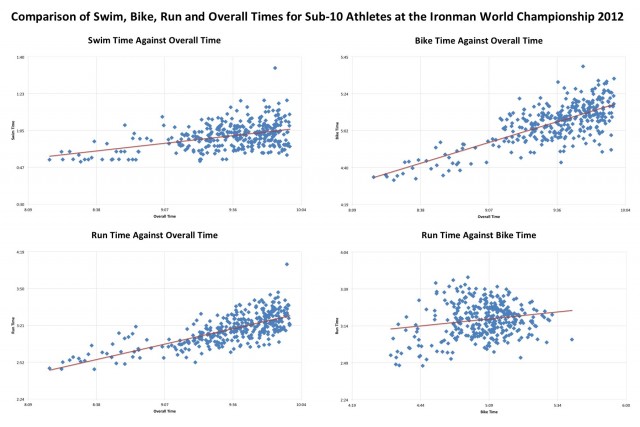
If we only consider the fastest athletes, which I’ll take to mean those going under 10 hours, then the relationships between the disciplines are remarkably similar for both races. Roth is faster, it is easier to break 10 hours there, but both have a high standard of fast athletes. As the chart below shows, in Kona the sub-10 athletes are again balanced. Notably the swim distribution is more tightly packed than for the equivalent athletes at Roth, selection at play once more or perhaps a side effect of the mass start. Perhaps it’s worth reflecting that the mass start may improve drafting opportunities during the swim and unfortunately increase the impact of drafting on the bike, we might expect both to lead to a tighter distribution of splits.
In my previous examination of the bike-run relationship I didn’t stop here, I attempted to find better evidence that a hard bike often leads to a slow run. Bear with me. I divided finishers into groups by percentage – 10% brackets from fastest to slowest, and then calculated the average bike splits for the fastest runners (top 25% of run splits in the group), slowest runners (bottom 25%) and the whole group. The idea being that if a hard bike leads to slower run we would expect to fine that the slowest runners tended to ride faster than the group average and the fastest runner tended to ride slower. Which is exactly what the data showed for Roth. Would I call it proof? No, but it offered a little support for a long held belief.
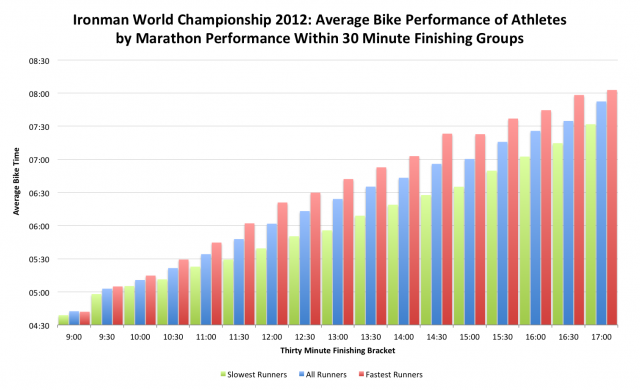
For Kona I’ve slightly altered my approach, dividing the field into fixed 30 minute blocks (with the exception of those going sub-9 who are grouped together). While the percentage approach ensured each group of finishers was of equal size, fixed finish times perhaps ensures groups contain a more comparable set of athletes. The results are in the graph below (you can also see a table of the data here)
As was the case in Roth the fastest runners have slower bike splits and the slower runners have faster bike splits; and as with Roth the question remains as to whether this is indicative of a relationship. It is worth noting that in the Sub-9 group, mostly male pros, there is little difference between the group average bike and the fastest runners’ average bike split, but as we spread back in the field the gap opens up. Also the faster an athletes finish time the smaller the difference between bike performance for different runners, a reflection of overall fitness and possibly better pace awareness. Of course swim and transitions being equal an athlete who runs 3:15 to finish in 9:45 must have biked more slowly than an athlete who runs 3:20 to finish in 9:45. As I said – this is not proof, more a potential indication. But if it is the case that those slower runners are biking too hard, the data shows that what they typically gain on the bike they more than lose during the run; their bike may be 5 minutes faster than the group average, but their run is 10 minutes slower.
Conclusions? The patterns I previously saw in the Roth results seem to be present in the Kona data, if there are differences then Kona is – questionably – more tightly bunched. Perhaps a subtle consequence of a mass start versus waves and the greater drafting and bunching opportunities that followed it, but equally potentially a reflection of the selective qualification process. Needless to say it remains the case that the fastest athletes are all round faster and that working too hard on the bike may really make you pay on the run.

Ironman Training Library
From nutrition to pacing - a collection of CoachCox blog posts focused specifically on Ironman training and racing.